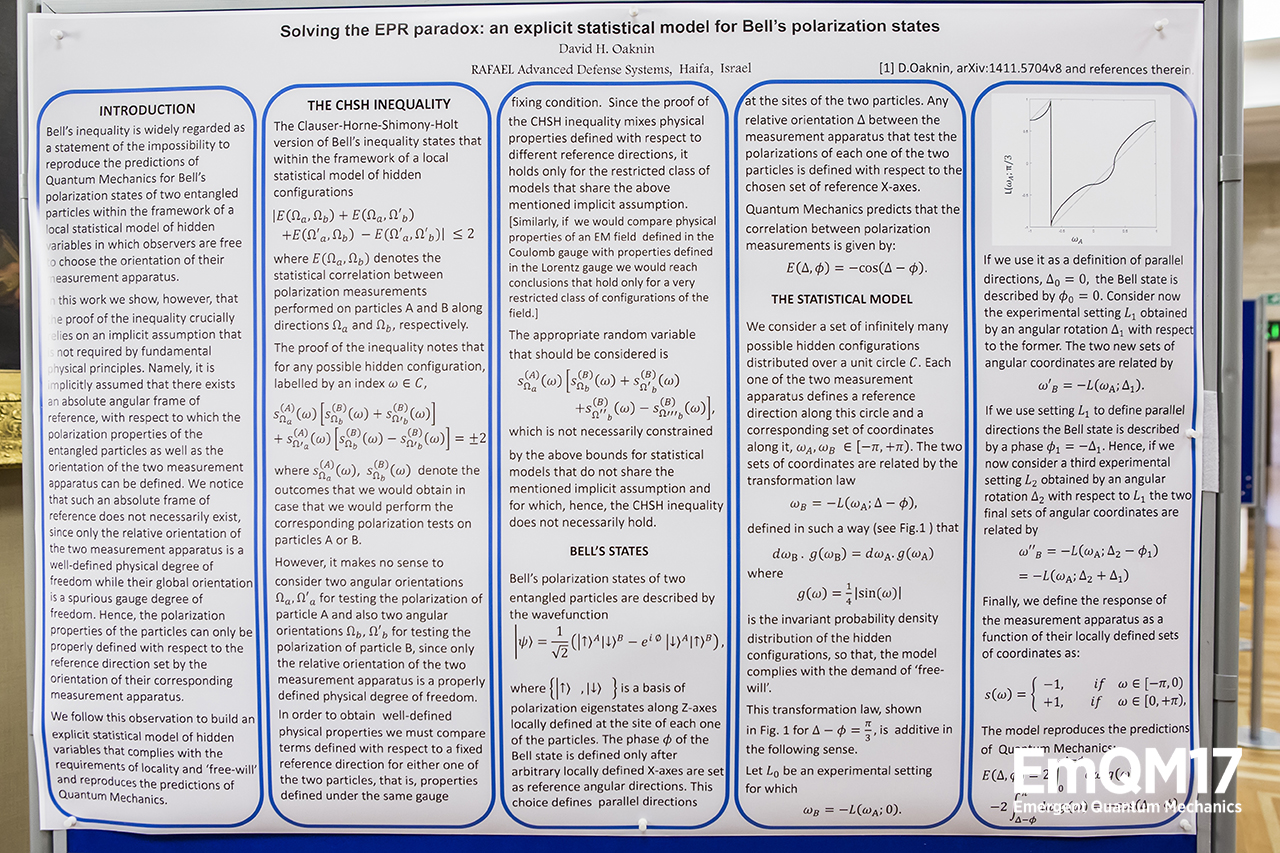
David Oaknin
Solving the Einstein-Podolsky-Rosen paradox: an explicit statistical model for the singlet polarization quantum state
The strong experimental evidence for the violation of Bell’s inequalities is widely interpreted as the ultimate proof of the impossibility to describe Bell’s polarization states of two entangled particles in terms of a local and realistic statistical model of hidden variables in which the observers are free to choose the settings of their measurements. In this paper we note, however, that Bell’s theorem relies crucially on a fourth implicit theoretical assumption, in addition to the explicit hypotheses of locality, physical realism and ‚free will‘. Namely, we note that the proof of Bell’s inequalities for generic models of hidden variables implicitly assumes that there exists an absolute reference frame of angular coordinates, with respect to which we can define the polarization properties of the hidden configurations of the pair of particles as well as the orientation of the measurement apparatus that test them. This implicit additional assumption, however, is not required by any fundamental physical principle and, indeed, it may be incorrect if the hidden configuration of the pair of entangled particles breaks the rotational symmetry along an otherwise arbitrary direction. We explicitly show that by giving up to this additional implicit assumption it is possible to build a local and realistic model of hidden variables for Bell’s polarization states, which complies with the demands of ‚free-will‘ and fully reproduces the quantum mechanical predictions. The model presented here offers a new insight into the notion of quantum entanglement and the role of measurements in the dynamics of quantum systems. It may help also to develop new tools for performing numerical simulations of quantum systems.